Automorphism groups of groups

After last week’s GAGA tutorials, I wrote some notes related to sheet 5.

Quadratic forms

A quadratic form is essentially the same thing as a symmetric bilinear form, at least over a field of characteristic different from 2. A while ago, I wrote a brief note on quadratic forms dealing with diagonalization and geometry. I hope it’s useful for HT2013, sheet 4, problem 8, in particular.

Orthogonal bases

I was a bit confused during tutorials today about orthogonal bases, so I wrote up a short note on how to find them. This method is illustrated with problem 5 on sheet 4 for Linear Algebra II.

Group theory tutorial, TT week 1 (=HT week 9)

I got quite confused with one of the problems in tutorial today. I had a glimmer of the right answer, but then misled myself into saying something quite silly. Anyways, here is a short note on this.

Symmetries

I have written some notes on symmetries following the Group Theory tutorials this week.

Collections, Hilary Term, 2012

I’ve marked the scripts for the algebra portion of the Merton collections for Mods Pure Maths, Part A AC1 and Part A AC2.
I am including here brief remarks on the questions. Later, if I have the energy, I will also upload comments on the Banach Spaces paper for Part B students.

POSTECH notes, algebra.

Here are some notes on

Automorphisms of algebraic number fields

to accompany the lecture on 5 December, 2011.

POSTECH notes on constructible numbers

Constructible numbers

Maximal ideals in Z[x]

Maximal ideals

Norms of elements and principality

Dear Professor Kim,

Sorry to bombard you with these questions. I have come across a problem on your note ‘some principle ideals’. When we factorize modulo 3 we get we then associate these factors with the ideals and respectively. When we compute the norm of we do so by calculating the determinant of the matrix and find that the norm is in fact 9, so is a principle ideal. However, we could just have easily used or and in each case I get a different answer for the determinant. Have I made an error or is there a canonical form of sort that I should be aware of?

Thank you for your time.

———————————————-

Reply:

First of all, I presume your etc. are etc. All the elements you mention do indeed belong to the ideal and can be used as generators *when used together with the element 3*. Indeed they are all all evaluations at of polynomials that are congruent to mod 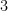. However, this does not mean they are generators on their own. Of course different elements in an ideal 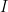will have different norms in general. However, an element is a generator *by itself* (making 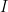into a principal ideal), exactly when . 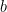Of course such a need not exist. I haven’t calculated the norms of the elements you mention, but if their norms come out larger than 9, it merely says they are not generators (again, by themselves), while is.

A thorny point that comes out of this discussion is that if you had initially presented the ideal as , for example, then it might have been harder to see that it is principal.