More Jordan bases and canonical forms

Dear Professor,

I have a couple of questions about the Jordan canonical form section of the course if you get a spare moment.
1. I understand that if are considering linear maps from a vector space over the complex numbers to another vector space over the complex numbers, then eigenvalues always exist. When we find a Jordan basis, we use these eigenvalues. Does this mean we are assuming that the field in question is the complex numbers? Surely if not, then these eigenvalues aren’t guaranteed to exist so we can’t always find a Jordan basis?

2. After finding a pre-Jordan basis, we have to replace some basis vectors so as to satisfy the condition that if 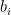belongs to , then belongs to for 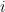greater than 1. I have noticed that sometimes there is a choice as to which basis vector in to replace. Does it matter? Is there a convention? Similarly, when extending our basis

for

to be a basis for , there may be a choice as to which basis vector we choose to add. Does it matter? Is there a convention? My questions above lead me to believe that there are actually infinitely many Jordan bases for any one linear map / matrix, but that their Jordan canonical form is unique up to permutation of the Jordan blocks. Am I correct in thinking this?

3. Finally, say we have a linear map with two eigenvalues, and Say the characteristic polynomial is

and the minimal polynomial is

with, obviously, less than or equal to , less than or equal to 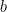. I don’t understand how we know without proof that . I have chosen a two eigenvalue case for simplicity – obviously I’m interested in all several eigenvalue cases.

Thanks very much!

Reply:

1. You are right that that eigenvalues need to be contained in the field of definition for a linear map to admit a Jordan canonical form. For example, the rotation matrix

will not have a Jordan canonical forms over . Over 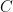, however, it is diagonalizable, and the diagonal form *is* the Jordan canonical form. (What is it?)

2. There is an error in the condition you write, which could be minor or serious. To be a Jordan basis for a linear map 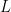with one eigenvalue , the requirement is that

for . Look carefully to see and understand the difference from what you wrote. (Actually, from the overall understanding reflected in your message, I suspect your mistake was just a misprint. But I wrote the above for the general reader.)

As to your question, you are write there there are many choices involved. This is the point people often find confusing, not just in this topic, but in many basic mathematical problems: when there is not a unique solution. We just have to understand the material well enough to feel relaxed about the choices. There is no general convention I can think of regarding `good’ choices, other than obvious demands of economy like simple numbers and as many zero entries as possible.

All of your remaining observations are correct. I wouldn’t be too surprised if a study of the *space of all possible Jordan bases* would yield some insight on good choices, at least in some natural special situations.

3. The general discussion is an obvious generalization of the case with two eigenvalues, so let’s stick to your question as it stands.

For , we have

and hence,

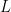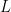Therefore, is stabilized (that is, taken to itself) by . Similarly, is stabilized by . By considering the shape of the Jordan canonical form for

(the one eigenvalue case) we see that

for . Similarly,

for . But we have

by the primary decomposition theorem. So

or

Therefore,

and

.

 

Spectral theorem etc.

Dear Professor Kim,

I have looked at your course summary and I cannot find anything about the Spectral Theorem. The proof of this theorem was not covered in class, and in the online notes it only says “See the article ‘The Spectral Theorem’ on the course webpage”. I have however seen that a question on this proof in 2006 paper, so I was wondering if we need still need to know this proof? Also, do we need to know the extra material on the course webpage such as the supplementary notes and articles?

Best regards,

———————————————

Reply:

The course summary definitely mentions the spectral theorem: On the list at the end, it is theorem 5.5.159, whose proof, as you point out, is in the supplementary notes. I hope the summary and the course blog is making the relative importance of different portions clear enough. Essentially all the supplementary material should be useful.
But perhaps most relevant are:

- A practical summary of the course

-The spectral theorem

-Remark on quadratic forms

-The first two pages of `Supplementary note on self-adjoint maps’

and the various example sheets on Jordan canonical forms.

 

Positive definite inner products

Hi Sir,

I’ve got another question.

When determining whether an inner product (in the Real space) is positive definite, we check it’s Real Canonical Form. If it’s diagonals are all “1″s, then it is positive definite. What about determining positive definiteness in the Complex space? I realised(from Sheet 8, Qns 1e) that the same method wouldn’t work (find the complex canonical form and see if its diagonal entries are all “1″s). How can we determine if an inner product is positive definite in the complex space?

—————————————————–

Reply:

Your observation is correct. Note that in the complex space, the positive definiteness is being checked for a *Hermitian* form, not a symmetric bilinear form (what is the difference?). Hence, the whole discussion of complex canonical forms does not apply. The only answer I can give at the moment is that you should think about the definition carefully. Of course there are the problems from the coursework, but it may help already to ask yourself: Is the standard Hermitian form on ,

positive definite? Why or why not?

 

Question on Bezout’s Lemma

For a question such as on Homework sheet 3 1ii.) and on some of the past papers, is it strictly necessary to use Bezout’s lemma? Would a simple substitution of and not suffice?

Also, would you get full marks for using a substitution instead of using Bezout’s Lemma.

Thanks

———————————————————-

Reply:

You would get full marks for any correct proof or answer clearly written.

Note that Bezout’s lemma is merely an `explicit Euclidean algorithm.’ As soon as and get at all large, you’ll find that the Euclidean algorithm is much more efficient than direct substitution. In some suitably general sense, the Euclidean algorithm is one of the most efficient algorithms around. It’s a bit of a miracle, in some sense.

However, your question is a good one. Check for yourself what the procedure of finding by substitution would involve.

 

Canonical forms and equivalence

Hi Sir,

just to make sure if I’m correct, is it true that if 2 symmetric matrices
have the same real and/or complex canonical forms then they are equivalent?
——————————————————————————-

Reply:

To be precise, two symmetric matrices are equivalent over if and only if they have the same real canonical form. They are equivalent over if and only if they have the same complex canonical form.

 

Question on isometries

Dear Professor,

Firstly thanks for taking the time out to reply to our messages, we really appreciate the help and guidance from yourself. I wanted to ask the following short question about the 2201 notes:

On page 56 Thm 5.4.150: after showing that and , can’t we simply show by saying:

and proceeding exactly as the last line of the proof at the bottom?

Thanks in advance.

——————————————————————

Reply:

Not quite. Although with a bit more argument it might be OK. In `the last line of the proof at the bottom,’ note that an unwritten step in the argument says

for *all* , and then one sets . This wouldn’t be admissible if we just had . Try it out to see clearly for yourself what I mean.

 

More general questions on 2201 exam

Hi

I was just wanted to ask you about the structure of the exam next week? (as I missed the revision session during Easter)

1) what will the layout be like? similar to 2008 paper?

2) how come the 2008 paper is different from previous years, the notation and the method of asking the questions seems different?

3) are there any key areas that will come up?

4) there are 5 chapters in the notes, will there be a question from each chapter? which chapter will have 2 questions from it?

Thanks for your time and I look forward to your reply

——————————————————

Reply:

I believe most of questions 1 and 3 have been answered in previous blog entries and the course summary. Regarding question 5, the questions will be reasonably well-distributed across the chapters as you might expect from any exam of this nature. Surely, I can’t tell you that some specific chapter will have two questions from it! I will say that about three of the questions may be distributed across roughly two of the chapters.

Regarding your question 2, you should look at the blog entries from around exam time last year to get some insight on this issue. The short answer is that if the 2008 exam looks very different from previous years, then you haven’t studied enough. This I mean quite seriously. At the level of scientific research, of course a conceptual breakthrough occurs when disparate phenomena are seen to be manifestations of the same principle. But even in a basic course, sufficient understanding is pretty well measured by the ability to see that rather large collections of problems are actually minor variations on the same theme. Certainly, don’t expect that the exam problems will be the same as the coursework or those of previous years with just the numbers changed!

 

Exam advice

Dr Kim

For those of us that unfortunately will not be able to make your revision classes for algebra 3, could you please tell us what you will be covering in those classes and could you please give any tips or advice for the upcoming exam.

Many thanks

——————————————————————–

Reply:

It’s somewhat difficult to summarize the revision session because it was based on questions from the audience, rather than following a prepared plan. You can get a sense of the questions that came up by reviewing this blog. Review also the blog entries from around exam time last year. Pretty much all the advice I gave then is still relevant.

 

Positive-definiteness

Dear Dr. Kim,

Could you show me how to determine whether it is positive definite for homework 8 question 1c please.
It will be very grateful if you can show me in your course blog.

Many thanks for your help.

——————————————————-

Reply:

The question takes the vector space to be the span of in , and the Hermitian form to be

We need to see if for all non-zero . But

as long as some is non-zero. So the form is positive definite. Notice that this form is actually defined and is positive definite on all of . In general if you have a Hermitian form on a -vectors space or a symmetric bilinear form on an -vector space, if the original form is positive definite, then its restriction to any subspace is also positive definite, simply by exmaining the definition of positive-definiteness.

 

Computing orders mod 23

Hi Sir,

Sorry to disturb you again. I was working out the order of 3 mod 23, which i found to be 11. I did this the following way:

I was wondering if there was a simpler method to find the order instead of doing it using this way?

——————————————————————

Reply:

It’s hard to give a general answer for small moduli, where the improvement over brute force calculation tends to be rather incremental. It might be somewhat helpful to analyze the *possible orders*. In the case at hand, the non-zero elements modulo 23 under multplication form a group of order . Thus, the possible orders of elements are 1,2, 11, and 22. Since 3 clearly doesn’t have order 1 or 2, the possibilities are 11 and 22. But I don’t see an obvious way to rule out the possibility of 22 without calculating as you’ve done. On the other hand, if any element satisfies

then we can immediately conclude that the order is 22.