Probability, Sheet 3, Problem 5

I’m sorry I’ve been falling behind on my blogging. I’ll try to catch up gradually. Here is a discussion of the problem, as I mentioned during the tutorial.

Probability, sheet 4, number 8

I didn’t have time to fully discuss number 8 of sheet 4 . But Matej Balog has kindly agreed to let me post his solution on the blog.

Probability sheet 4, number 9

I would like to highly recommend working out number 9 on probability sheet 4, simply because it’s so amusing.

It reads like this:

———————————-
Passengers arrive at a bus stop at rate 1 per minute. Find the distribution of the number
of passengers boarding a typical bus in two cases: (a) buses arrive regularly every 10
minutes; (b) buses arrive as a Poisson process with rate 1 per 10 minutes. Which one has
higher variance?

I arrive at the bus stop at 2pm. Find the distribution of the number of other passengers
boarding the same bus as me in the two cases above.
———————————

Most of the problem is straightforward, and I won’t go over it here. For example, the mean number of passengers boarding will be 10 in either case, but, naturally, the variance will be higher in case (b). But what’s amusing is the second part, where we assume you arrive at the bus at some given time, and calculate the mean number of *other* passengers boarding with you. For case (a), you find 10 as before, but for case (b), the mean turns out to be 20!

This situation is sometimes referred to as the ‘inspector’s paradox’. That is, if you’re an inspector trying to check up on the mean number of passengers boarding at a given stop by arriving at 2 PM for a number of days to take the bus, you will tend to find a larger mean than the true mean for the average bus, at least in the model (b). You should ask yourself why this happens.

Probability sheet 4

Here is a sketch of problem 10 on sheet 4. The convergence question that came up in the tutorial is clarified in an elementary way.

Added: Towards the end of the document, I should have stated that is a Riemann sum for the integral with mesh size , Since this goes to zero and we are integrating a continuous function, we get convergence of the sum to the integral.

Probability, week 7

I’ve asked David Steinsaltz about problem 5 (b) in sheet 3, and he tells me that he stated a theorem (13.7) last week that allows you to compute long term averages using stationary states even in the non-ergodic case.

Recall that the problem is to compute

The probability can be written as , where and 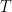is the transition
matrix. The theorem says that this limit is the same as the average distance for the stationary distribution, which is 3/2.

One way to reduce this problem to the ergodic case is to note that the processes that act as 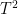on the odd distance states and the even distance state separately are both ergodic. If you compute the stationary states in these cases, you will note that the average distance for both stationary distributions is 3/2. Hence, the limit above will also converge to 3/2.

Yet more remarks on Probability A, sheet 1

I am adding yet more remarks on sheet 1 of Probability A, this time on question 6.

Probability, more remarks

I am adding now some comments on problem 5 of the probability sheet 1.

Probability tutorials, week 3

Here are some remarks on the probability tutorials last week. I didn’t have time to comment on any but the most elementary problems, but I thought it might be good to review the basics anyways. I’ll try to write more this weekend.