Location for office hours, 5 May, 2008

There was an earlier post about special office hours for last minute questions on algebra 3. But I had forgotten about the public holiday. So I looked around for some public space where we could meet, and it seems the main library will be open.

Therefore, on 5 May from 11-12 and 2-3, instead of the math lounge, I will be sitting in the Flaxman gallery (the round room with sculptures) to answer questions.

Best,

Minhyong Kim

Non-isomorphic groups

Dear Dr. Kim,

I am having a few problems with regards to some work on groups. I would like to know how to find isomorphically distinct groups in the context of a semi-direct product, given a number of possible homomorphisms.

Is it enough to show that if the center’s of each possible group are distinct?

If so, how would you find the center of semidirect product with C_10 x C_4 as the underlying set with h:C_4 –>Aut(C_10) a homomorphism, such that h(y) = phi_9, y belongs to C_4, phi_9 belongs to Aut(C_10).

I am aware that the centre is the fixed point set acting on itself by conjugation, however when I try to evaluate this set, denoted Z(g), I can only find that 1, x^5 belong to Z(g) where x^5 belongs to C_10. I have seen elsewhere that the center of this set is isomorphic to C_2 x C_2 but am unable to compute this. Do you see what I have overlooked?

Is this the most efficient way to find distinct groups and eliminate those that are not? I have seen some examples where two groups where found to be the same under a change of variable. Are there any rules or guidelines to take into account when looking for these things, or is it just a matter of remembering them?

Thanks very much for your time.

Reply:

I will answer the last question first: No mathematical problem is solved only by remembering a number of facts. Of course there are principles. Most importantly, make sure you understand the definitions. Your characterization of the center Z(g) is rather poorly phrased, but also rather too sophisticated in most concrete situations (although it may be useful in certain general theorems like the Sylow theorem). You should rather make sure you know the simple definition: Z(g) is the subset of g consisting of elements that commute with all elements of g. In symbols,

Try to use this to compute the center of the group you describe above. In this regard, it is convenient to note that the group is generated by the elements (1,0) and (0,1). So an element x=(m,n) is in the center if and only if (m,n)(1,0)=(1,0)(m,n) and (m,n)(0,1)=(0,1)(m,n). If you just use the definition of the semi-direct product carefully, the rest should be easy.

Here are some general remarks in relation to the problem: To check if G_1 and G_2 are isomorphic, you should go through some features of groups that are preserved under isomorphisms. Typically, you start with the most simple-minded features and progress to more sophisticated ones. For example, if I ask you if C_5 and C_7 are isomorphic, you should be able to say right away that they are not, simply because they have different numbers of elements. That is, the cardinality of a group is preserved under isomorphism. How about S_3 and C_6? They are not isomorphic because one is commutative and the other is not. Again, the point is that the property of being commutative is preserved under isomorphism. After this, things can become considerably more complicated, depending on the example. But the criterion of computing the center is a good one: if G_1 and G_2 are isomorphic, then Z(G_1) and Z(G_2) are isomorphic. Therefore, if Z(G_1) and Z(G_2) are *not* isomorphic, then G_1 and G_2 are not isomorphic. Of course, this is useful only if it’s easier to distinguish Z(G_1) and Z(G_2) than to distinguish G_1 and G_2 directly. But it’s plausible that there is an `inductive’ structure to the problem, in that if the groups involved are non-abelian, then the centers are smaller than the original groups and furthermore, abelian, and therefore, easier to analyze.

The general problem of distinguishing groups can eventually involve a great deal of ingenuity and knowledge. For example, if and are isomorphic, it can be quite complicated. One good way to get a feel for such problems is via constructing yourself some tricky examples. Can you come up with 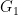and that are definitely non-isomorphic, but for which and ?

Ideal inverses

Hi Sir.

Should be a quick question about fractional ideals.

How does one work out the inverse of an ideal, when the ideal is generated by multiple elements (esp. 2 elements). i.e. I am looking to work it out intuitively, instead of a fool-proof method for lengthy ideals.

Thanks.

(you have an example in ufd.pdf where you quoted the inverse of

to be

Reply:

As you’ve guessed, there is a foolproof method using integral basis for ideals. But perhaps it’s not worth going into the general algorithm now.

In the example you mention, if you read the previous paragraphs carefully, you’ll see that actually, . That’s why . But for fractional ideals that are not principal, it can be trickier to find inverses easily. Here is my suggestion for now: When we factorize elements, we find relations of the form

But then, we see that

For example, in , we find

where

(I think the are non-principal, but I’m too lazy to check at the moment. In any case, they are not obviously principal, which is all that matters for the present demonstration.)

Therefore,

The idea here is the same one that recurs many times in the theory. To get information about an ideal, try to make it occur in the factorization of some principal ideal.

Office hours

I will be in the fifth floor common room from 11-12 and 14-15 on 5 May for last minute questions on algebra 3.

I’ll also be in my office most of the day on 2 May and 15-17 on 5 May.

Jordan basis

Hi Sir

I was looking at 2006 qs 4c) which asks me to find the Jordan Canonical Form of D, where

V= {a0 + a1x + a2x^2 : a0, a1, a2 in C}

and D: V–>V defined as D(f) = d^2f/dx^2 – 4f

I have been looking at Homework 4 and 5 to help me with this but both examples are without the 4f.

I want to find ch(x). If we have polys of deg <= 2 we need to differentiate 3 times to get 0. So D^2 will give me 0. But D^2(a0 + a1x + a2x^2) = -4(a0 + a1x + ax^2)

(I hope I am correct in thinking that f= a0 + .. regardless of the power of D) So for this to be 0 we need a0 = 0 and x=0. From here I am not sure how to go about finding ch(x) and m(x) (I would guess that ch(x) = x^3 and m(x)= x^2 but without much confidence or knowledge), would you be able to help me on this?

Thank you

Kind Regards

Reply:

There are many mistaken statements above. For example, D is not just differentiation, so no power of it needs to be zero.

Let me suggest one easy way to do this problem. Presumably, you know how to find the Jordan canonical form and Jordan basis for a 3 by 3 matrix. Can you turn this problem into one about such a matrix? However, remember that the eventual Jordan basis needs to be expressed in terms of elements of V.

Ask again if you run into trouble.

Factorization

Thank you, I think I understand. But if p_i=(p,f_i(a)) is a maximal ideal, is (p) the prime ideal? And where do principal ideals come into this?

For example in exam paper 2002, question 3 says to factorise into prime ideals. Is the answer ? And on question 4 we are factorising into maximal ideals, is this the same method?

I hope this makes sense!

Thanks

Reply:

You should review chapters 16 to 21 very thoroughly. I’ve also written up some

Factoring in algebraic number fields

Hi,

I was wondering if you could explain how to factorise ideals into prime and maximal ideals.

Also how do you calculate norms of ideals, as I have the definition N(I)=|Ok/I|, but I dont reall understand what this means.

Thanks for your help

Reply:

The main tool we’ve been using is Dedekind’s prime factorization theorem. Look at theorem 160 from the notes and examples 162 and 163 following it. There are a number of other examples in the optional coursework.

For a non-zero ideal I inside the ring O_K of algebraic integers inside a number field K, the notation

|O_K/I|

refers to the number of elements inside the quotient ring O_K/I.

If you would like to understand this, you can find computations in the examples mentioned above. You can even try easier ones:

-Take K=Q so that O_K=Z. What is the norm of the ideal (10)?

Inside Z[i], what is the norm of the ideal (2)? What about the ideal (1+i)?

Redundant question on 2201 exam

Dear sir,

When reading through the web notes i came across a section 2.2.31 that says it has not been covered in class. I was wondering if we were required to know this proof for reproduction in the exam, or just to enhance our knowledge.

Also, having been through previous exam papers I was wondering if the proofs that were asked for in these papers would be needed in your exam (the ones not covered in class).

I have also heard from people who had come to see you about the possible percentages of proofs to application questions that may arise in your paper, is it possible to clarify how many marks could possibly gained through theory alone (without application).

Thanks very much,

Regards

Reply:

I chose the title for this post because most aspects of this question have been dealt with in previous posts. I won’t point to the specific ones because reading through many of them should be a useful exercise. I strongly urge everyone to read through the previous posts. In their entirety, I believe they provide a reasonable feel for the exam.

I will reply here to the last question: It’s hard to give a precise percentage because it depends on which questions you choose, how the whole paper looks and so on. But I can say that if you just memorize perfectly the proofs in the notes but have no understanding of how they work or how they might be applied, your score will probably be dangerously low.

2201 exams

Dear Prof Kim

is fermat’s little thm included

2006, 2007 past papers are similar, 2005 confuses me a bit with the style of the questions; i know the same knowledge is required but the style of the question makes it easier for me to understand what exactly the question is asking; which set is closer to your style

you divided the paper saying one question each from first three topics and three form the last two; 1) number theory 2) polynomial rings 3) JCF – 1 question each 4) bilinear and quadratic forms 5)inner product space – 3 from these two; plz confirm

kindest regards

Reply:

(1) Yes, Fermat’s little theorem is critical to much of the material on congruences. (Obviously, a reply like this does not guarantee that you will be examined on it.)

(2) Regarding the past exams, I don’t want to directly contradict your impression, but it might be most informative for you if I say honestly that I don’t see a real difference in style between 2005 and 2006. (Which is what I have access to at the moment. I’m in Bordeaux right now.) If you would like to formulate more precisely what the confusion is, I can try to help more.

(3) The distribution of problems you describe is correct.

Congruence of forms

Hi Professor Kim,

I was just wondering how you determine whether two quadratic forms q and r are congruent over R and C. I know that you proceed by finding their canonical forms by doing double elementary row and column operations, but what do you do next? Are they congruent if they have the same canonical form over R (or over C) OR is this the definition of being equivalent. Please help.

Thank you very much.

Reply:

Two forms q_1 and q_2 are congruent if any of their representing matrices A_1 and A_2 are congruent. Notice that this definition doesn’t depend on the choice of representing matrices. (Why not?) Of course, it suffices to diagonalize (in the sense of congruence, i.e., using double operations) A_1, A_2 and then check if the diagonal matrices are congruent. This can still be hard. But over R or C,

A_1 and A_2 are congruent if and only if their canonical forms are *equal*.

This is a very useful criterion, since we can trivially check two matrices for equality.