Some points on an elliptic curve

The elliptic curve is , which has the obvious point . This file displays the denominators of the -coordinates of the points . This was discussed in my course ‘Topics in Mathematics,’ Summer, 2016, at Ewha Womans University.

Rotations and reflections

A brief  note.

Grothendieck

Click to access grothendieck2.pdf

Axiom

Text of comments on the sculpture ‘Axiom’ by Mat Chivers at the unveiling ceremony on 28 October, 2014 at the Andrew Wiles building in Oxford:

Click to access chivers.pdf

Madrid Lecture

Click to access madrid2014.pdf

Probability, Sheet 3, Problem 5

I’m sorry I’ve been falling behind on my blogging. I’ll try to catch up gradually. Here is a discussion of the problem, as I mentioned during the tutorial.

A vector space of uncountable dimension

Let be the real vector space of all functions from the natural numbers to the reals. Then 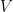has uncountable dimension. To see this, for each , let 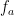be the function such that .

Claim: The are linearly independent.

Proof: It suffices to show that any finite collection with a strictly increasing sequence of 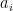are linearly independent.

We prove this by induction on , the fact being clear for 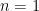. Suppose with . The equation means

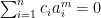
for all 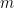. Thus, for all 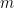. Now let . This shows that . Thus, by induction, all .

We have displayed an uncountable linearly independent collection of functions in 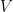. Now, let be a basis for 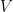. For each 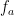there is then a unique finite set of indices such that 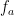can be written  as a linear combination with non-zero coefficients of . The linear span of any given finite set of the is finite-dimensional. Hence, for any finite subset , there are at most finitely many such that . That is, the map is a finite-to-one map from the positive reals to the finite subsets of 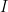. Hence, the set of finite subsets of 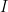must be uncountable. But then 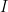itself must be uncountable. (I leave it as an exercise to show that the set of finite subsets of a countable set is itself countable. You should really write out the proof if you’ve never done it before.)

I might point out that before the tutorials, I was a bit confused myself. That is, the first bit about the 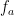‘s being an uncountable linearly independent set is rather easy. However, I started hesitating: Still, why can’t there be a countable set of elements in terms of which we can express all of them? After all, the set of coefficients we can use for the expressions is uncountable… So think through again clearly: how is this resolved above?

As a final remark, note that this proves that 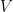is not isomorphic to . This is perhaps the first example you’ve seen where you can prove that two vector spaces of *infinite* dimensions are not isomorphic by simply counting the dimensions and comparing them.

Linear independence of polynomials

One of the exercises this week asked for a proof of linear independence for the set

inside the polynomials with real coefficients. However, note that the polynomials here are regarded as *functions* from to . Thus, it amounts to showing that if

as a function, then all have to be zero. This does require proof. One quick way to do this is to note that all polynomial functions are differentiable. And if

is the zero function, then so are all its derivatives. In particular,

for all . But Thus, for all .

One possible reason for confusion is that there is another ‘formal’ definition of by simply identifying a polynomial with its sequence of coefficients. That is, you can think of an element of as a function that has *finite support* in that for all but finitely many . With this definition, the polynomial becomes identified with the function that sends to 1 and everything else to zero. If you take this approach, the linear independence also becomes formal. But in this problem, you are defining as a function in its variable. This of course is the natural definition you’ve been familiar with at least since secondary school.

Here are two questions:

1. If you think of two polynomials and as functions from to with finite support, what is a nice way to write the product ?

2. What is the advantage of this formal definition?

Mathematics in Society

After several conversations recently about the social status of mathematics, I thought I’d put here links to two short essays I wrote on this.

1. An exchange on Mathoverflow

2. Mathematical Vistas

Mathematical problems

This week, I was given a very short deadline to write one of those introductory blurbs to the Korean edition of Ian Stewart’s book, ‘The Great Mathematical Problems.’ I could only skim through it, but I managed to get enough of a sense to write something. Here it is, in case some students find it interesting.